اگر الگوریتم‌های جست و جو را بررسی کنید، حتما با الگوریتم *A روبه‌رو خواهید شد. اگر بیشتر در قلمرو این دسته از الگوریتم‌ها بررسی داشته باشید، ممکن است به الگوریتمی با نام (Iterative Deepening A*‎ | ‎IDA*‎) برخورد کنید. اگرچه این الگوریتم‌ها برای افراد ناآشنا با الگوریتم‌های جست و جو، پیچیده به نظر می‌رسند، اما با صرف زمان و بررسی چند مثال به‌همراه پیاده‌سازی، درک این الگوریتم‌های قدرتمند به طرز شگفت‌آوری ساده می‌شوند. در این مطلب از مجله فرادرس می‌خواهیم به یکی از الگوریتم‌های جست و جوی آگاهانه به نام الگوریتم *IDA بپردازیم که زیرمجموعه‌ای از الگوریتم‌های پیمایش گراف و جستوی مسیر به‌ شمار می‌آید.

الگوریتم *IDA هم مانند سایر الگوریتم‌های جست و جو وظیفه یافتن کوتاه‌ترین مسیر بین یک «گره» (Node) ‌مشخص از گراف به هر یک از گره‌های هدف موجود در یک گراف وزن‌دار را بر عهده دارد. IDA*‎ یک الگوریتم جست و جوی عمقی تکرار شونده است که یکی از زیر شاخه‌های الگوریتم A*‎ است و مشکل پیچیدگی فضایی الگوریتم A*‎‎ را تا حدی حل کرده است. ما ابتدا نگاه مختصری به مفهوم الگوریتم جست و جو، انواع و ویژگی‌های اصلی آن خواهیم داشت و در ادامه مروری بر الگوریتم A*‎‎‎ خواهیم داشت و سپس ‎IDA*‎ را به‌طور کامل معرفی و با A*‎ مقایسه می‌کنیم.

مروری بر الگوریتم جست و جو

الگوریتم‌های جست و جو برای حل مسائل جست و جو در هوش مصنوعی مورد استفاده قرار می‌گیرند. به‌طور کلی مسئله جست و جو با سه مورد فضای جست و جو، وضعیت اولیه و وضعیت هدف تعریف می‌شود. الگوریتم‌های جست و جو با استفاده از دنباله‌ای از اقدامات، از وضعیت اولیه به وضعیت هدف می‌رسند و با بررسی تمام حالت‌های ممکن، بهترین راه‌حل را برای مسئله پیدا می‌کنند. بدون وجود این الگوریتم‌ها، ماشین‌ها و برنامه‌های کاربردی هوش مصنوعی نمی‌توانند راه‌حل‌های مناسب را پیدا کنند.

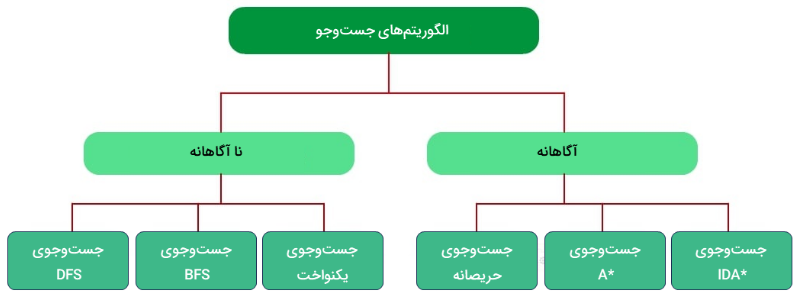
الگوریتم‌های جست و جو به ۲ دسته کلی تقسیم می‌شوند که در ادامه آورده‌ایم.

•  الگوریتم‌های آگاهانه: شامل الگوریتم‌های هیوریستیک یا «ابتکاری» (Heuristic) هستند که برای به دست آوردن گره هدف از یک سری اطلاعات استفاده می‌کنند. می‌توان گفت که این دسته از روش‌ها در حل مسائل پیچیده بهتر عمل می‌کنند. البته پیش‌تر نیز در مجله فرادرس راجع به جست و جوی هیوریستیک مطالبی را ارائه کرده‌ایم.
•  الگوریتم‌های ناآگاهانه: این دسته از الگوریتم‌ها که «الگوریتم‌های نابینا» (Blind Algorithms) نیز نامیده می‌شوند برای انتخاب حالت بعدی، از معیار ارزیابی استفاده نمی‌کنند.

لازم به یادآوری است که الگوریتم «هیورستیک» (ابتکاری | Heuristic)، روشی را به‌کار می‌برد که در آن نسبت به الگوریتم‌های کلاسیک عملکرد سریع‌تری دارد. همچنین در موارد زیر می‌توانند جایگزین مناسبی برای این دسته از الگوریتم‌ها باشند.

• هنگامی‌که الگوریتم‌های کلاسیک توانایی یافتن را‌ه‌حل در زمانی معقول را ندارند.
• زمانی‌که پیدا کردن جواب دقیق در فضای جست و جو برای الگوریتم‌های کلاسیک امکان‌پذیر نیست.

خصوصیات اصلی الگوریتم جست‌ و جو

به‌طو‌ر کلی، استاندارد بودن یک الگوریتم جست‌ و جو با ۵ ویژگی اصلی بیان شده در زیر معنا پیدا می‌کند.

• «کامل بودن» (Completeness): الگوریتم جست و جو در صورتی کامل است که – در صورت وجود یک راه‌حل – تضمین کند راه‌حلی را در زمانی محدود پیدا می‌کند.
• «بهینگی» ‌(Optimality): یک الگوریتم را در صورتی بهینه می‌دانیم که تضمین کند بهترین یا مقرون به صرفه‌ترین راه‌حل را در صورت وجود پیدا می‌کند.
• «مقبولیت» (Admissibility): در «جستجوی آگاهانه» (Informed Search)، مقبولیت به ویژگی یک تابع هیوریستیک اشاره دارد که هرگز هزینه دست‌یابی به هدف را بیش از مقدار واقعی تخمین نزند. تابع هیوریستیک دارای مقبولیت، تضمین می‌کند که الگوریتم جستجوی آگاهانه، راه‌حل بهینه را پیدا خواهد کرد.
• «پیچیدگی زمانی» (ُTime Complexity): این ویژگی، بیشینه زمان مورد نیاز برای حل مسئله را بیان می‌کند.
• «پیچیدگی مکانی» (Space Complexity): این خصوصیت بیان‌گر حداکثر حافظه یا فضای ذخیره‌سازی مورد نیاز هنگام انجام عملیات جست و جو است.

 معرفی الگوریتم A*‎

الگوریتم A*‎، الگوریتمی هیوریستیک به‌شمار می‌رود که با تلاشی مؤثر به‌دنبال پیدا کردن گره «مقصد» (Goal) است. این الگوریتم در هر مرحله از مسیر خود ۳ معیار مختلف فهرست شده در ادامه را اندازه‌گیری می‌کند.

• هزینه G
• هزینه H
• هزینه F

هزینه G

هزینه‌ای که نیاز است تا الگوریتم از گره شروع به گره فعلی برسد، «هزینه G» نامیده می‌شود. به زبان ساده این هزینه، میزان دور بودن گره جاری از گره شروع را نشان می‌دهد. برای مثال اگر برای رسیدن از گره شروع به گره جاری ۵ واحد نیاز باشد، مقدار هزینه G برابر با ۵ خواهد شد. اما توجه داشته باشید که مقدار این هزینه همیشه برابر با فاصله ۲ گره نخواهد بود چون گاهی ممکن است موانعی در مسیر موجود باشند که نیاز است تا در نظر گرفته شوند.

هزینه H

هزینه تخمینی برای رسیدن از گره جاری به گره هدف «هزینه H» نامیده می‌شود. تخمین و محاسبه این معیار در مسیریابی‌های پیچیده‌تر ممکن است سختی بیشتری به‌دنبال داشته باشد. اما به‌طور کلی این معیار نیز میزان دور بودن گره جاری از مقصد را نشان می‌دهد. برای مثال، اگر در این مورد هم گره جاری تا گره هدف ۷ واحد فاصله داشته باشد – حتی در صورت وجود مانعی بر سر راه – می‌توان هزینه H را برابر با مقدار ۷ در نظر گرفت. به‌طور کلی، این معیار  به عنوان حداقل فاصله گره جاری تا گره هدف در نظر گرفته‌ می‌شود.

 هزینه F

این معیار در واقع، هر ۲ هزینه G و H را به منظور دستیابی به هزینه کلی رسیدن از گره جاری به گره هدف، با هم جمع می‌کند.

در الگوریتم A*‎، علاوه بر به‌دست آوردن این ۳ معیار در هر گره باید مسیر بهینه از گره شروع تا گره جاری ذخیره شود. به این ترتیب می‌توان هنگام دسترسی به هدف، مسیر بهینه را از طریق تمامی گره‌های پیموده شده از گره هدف تا گره شروع، بازیابی کرد. این الگوریتم، مجموعه‌ای از مراحل بسیار ساده‌ای را دنبال می‌کند که در ادامه به اختصار به آن پرداخته‌ایم.

الگوریتم در ابتدا و در گره شروع، هر ۳ هزینه را برای گره‌های مجاور محاسبه می‌کند. در ادامه،‌ گره‌‌ای انتخاب می‌شود که کمترین مقدار هزینه F را داشته باشد و این فرایند دوباره تکرار می‌شود. هنگامی‌که الگوریتم به گره‌ای با هزینه H صفر رسید،‌ آنگاه یعنی به گره مقصد رسیده است. با دستیابی به گره هدف، الگوریتم A*‎ با انجام عمل «بازگشت به عقب» (Back Tracking) مسیر مبدا تا مقصد را پیدا می‌کند.

تصویر آورده شده در ادامه، نحوه عملکرد الگوریتم A*‎ را نشان داده است. در این تصویر، گره‌های سبزرنگ «گره‌‌های باز» نیز نامیده می‌شوند، به این معنا که مقدار هزینه برای این دسته از گره‌ها محاسبه شده است اما چون در تمامی گره‌های باقی‌مانده، گره‌هایی با هزینه F کمتری هم وجود دارند، تا این لحظه گسترش پیدا نکرده‌اند. لازم است توجه داشته باشیم که گره‌های قرمزرنگ یا «گره‌های بسته» گسترش یافته‌اند اما به‌عنوان گره هدف تشخیص داده نشده‌اند.

الگوریتم *IDA‎ چیست؟

الگوریتم *IDA برای یافتن مسیر بهینه از روش «تکرارشونده عمقی» (Iterative Deepening) استفاده می‌کند که که این سیاست باعث می‌شود تا نسبت به الگوریتم A*‎ برای ردیابی مسیرها از میزان حافظه کمتری استفاده کند. این استفاده از حافظه کمتر به ویژه زمانی به وجود می‌آید که تعداد گر‌ه‌های باز بیشتری برای بررسی داشته باشیم. در روش A*‎‎‎‎، کل فضای جست و جوی بررسی‌ شده، در حافظه نگهداری می‌شود که این مورد در فضای‌های جست و جوی بزرگ ممکن است با چالش همراه باشد. این الگوریتم به‌جای نگهداری کل فضای جست و جوی بررسی‌شده، در هر تکرار، تنها به ذخیره مسیر طی شده تا گره جاری و هم‌چنین هزینه‌های مربوط به آن می‌پردازد و به منظور پیمایش در فضای جست‌ و‌ جو از روش «اول عمق» (Depth First) استفاده می‌کند.

با این حال، روش IDA*‎ به‌دلیل رویکرد جست و جوی مورد استفاده، نسبت به A*‎، کند‌تر عمل می‌کند. مهم‌ترین دلیلی که برای کند بودن سرعت این الگوریتم می‌توان بیان کرد این است که IDA*‎ نیاز دارد تا به‌صورت مکرر گره‌های مشابه را در فضای جست و جو گسترش دهد. این الگوریتم در هر تکرار، فضای جست و جو را با در نظر گرفتن محدودیت تعیین شده به‌صورت عمقی جست و جو می‌کند و ممکن است گره‌ها را به دفعات بازبینی کرده و گسترش دهد که این نیز پیچیدگی زمانی را بیشتر می‌کند.

مراحل اجرای الگوریتم *IDA به این شکل است که ابتدا هزینه H را برای گره شروع محاسبه می‌کند و آن را به‌عنوان مقدار «آستانه» (Threshold) در نظر می‌گیرد. در ادامه نیز، تنها گره‌های دارای هزینه F کمتر یا مساوی با مقدار آستانه را از طریق پیمایش عمقی گسترش می‌دهد. به بیان دیگر، IDA*‎، جست و جوی عمقی را به گونه‌ای انجام می‌دهد که در هر مرحله، گره‌هایی با مقادیری بیش از مقدار آستانه تعیین‌شده، هرس شوند.

بدین‌ترتیب در IDA*‎ با رسیدن به گره هدف می‌توان گفت که بهترین پاسخ پیدا شده است. در ادامه کار، این الگوریتم، مسیر بهینه را در همان «پشته» (Stack) فعلی – که شامل همه گره‌های مسیر فعلی است – پیدا می‌کند. در غیر این صورت، مقدار آستانه را به میزان کمترین هزینه گره‌های گسترش‌نیافته، افزایش می‌دهد. سپس این روند را تا هنگام پایان الگوریتم‎ یا هنگام بروز شکست – عدم یافتن راه‌حل – تکرار می‌کند. تصویری که در ادامه آورده شده، نحوه کار الگوریتم *IDA را به‌خوبی نشان می‌دهد.

در این مثال، عملکرد کند الگوریتم *IDA را به‌وضوح می‌توان مشاهده کرد. همان‌طور که پیش‌تر هم بیان کردیم، این الگوریتم در مقایسه با A*‎ سرعت پایین‌تری دارد. چون الگوریتم A*‎ هر گره باز را تنها یک مرتبه بررسی می‌کند و سپس آن گره بسته می‌شود. در حالی‌که IDA*‎ ممکن است همان گره را تعداد دفعات بیشتری – هزار، ده‌هزار یک‌میلیون بار یا حتی بیشتر – پیش از رسیدن به راه‌حل بررسی کند. با این وجود، همان‌طور که پیش‌تر هم بیان شد، به‌کارگیری بهینه حافظه، یکی از دلایلی است که در برخی موارد باعث برتری این الگوریتم نسبت به A*‎ می‌شود.

هنگامی‌که A*‎ گره‌ای را گسترش می‌دهد، به‌طور معمول، گره‌های بیشتری را به فهرست گره‌های باز اضافه می‌کند. بنابراین به‌کارگیری الگوریتم A*‎ در «فضا‌های جست‌ و جوی بزرگ» (Massive mazes) – به‌خصوص هنگام محدود بودن حافظه – می‌تواند بسیار چالش برانگیز باشد. این در حالی است که در «فضاهای جست‌ و جوی محدودتر ولی با مسیری پیچیده‌تر» (Confined or Roundabout mazes)، استفاده از A*‎ انتخاب بهتری محسوب می‌شود زیرا در این نوع مسیرها عملکرد IDA*‎ به شدت کند می‌شود. در وب‌سایت PathFinding.js «+» می‌توانیم آزمایش‌های بیشتری را در این مورد بررسی کنیم. به این صورت که مسیرهای دلخواه – از نظر پیچیدگی – را ایجاد و الگوریتم‌های جستجو مانند IDA*‎ را روی آن اجرا کنیم.

مراحل گام به گام اجرای الگوریتم *IDA

در ادامه، گام‌های اجرای الگوریتم جست و جوی IDA*‎ را آورده‌ایم.

1. تعیین مقدار «آستانه» (Threshold): ابتدا مقدار آستانه‌ای برابر با هزینه هیوریستیک تخمینی از گره شروع تا هدف، تعیین می‌شود.
2. جست و جوی اول عمق با در نظر گرفتن مقدار آستانه: از گره شروع و با در نظر گرفتن محدودیت آستانه، جست‌و‌جوی اول عمق انجام می‌شود. به بیان دیگر، هر گره‌ای که هزینه F  آن بیشتر از مقدار آستانه باشد، هرس می‌شود.
3. بررسی گره هدف: در صورت پیدا شدن گره هدف در حین فرایند جست و جو، مسیر بهینه تا هدف را به عنوان خروجی برمی‌گرداند.
4. به روز رسانی مقدار آستانه: در صورت پیدا نشدن گره هدف در حین فرایند جست و جو، IDA*‎، مقدار آستانه را به میزان کمترین هزینه در میان گره‌های هرس شده افزایش می‌دهد.
5. تکرار مراحل تا دستیابی گره هدف: الگوریتم، مراحل پیشین را تکرار و تا یافتن گره هدف، مقدار آستانه را به‌روز‌رسانی می‌کند.

مثالی از پیمایش الگوریتم *IDA‎‎ در یک گراف

در مثالی که آورده‌ایم، مراحل گام به گام اجرای الگوریتم *IDA‎‎ را در یک گراف نشان داده‌ایم.

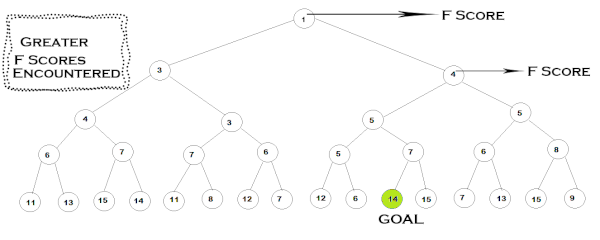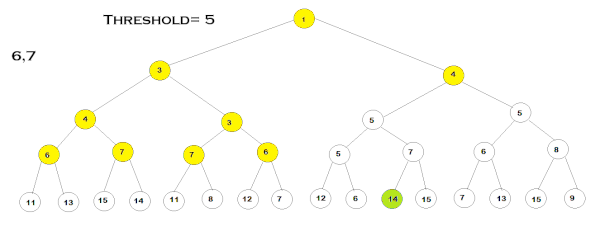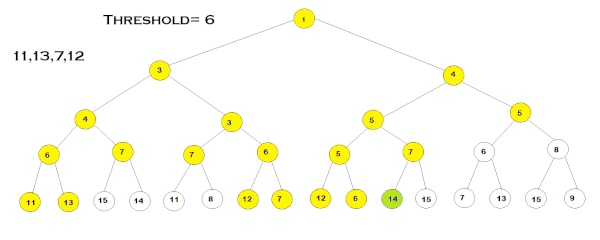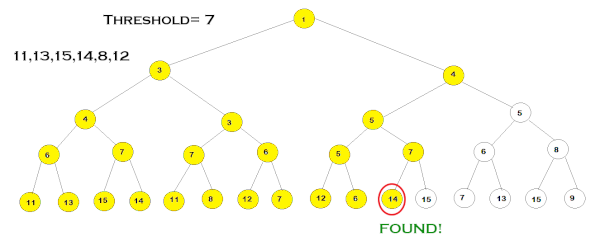
مقادیر نوشته شده روی هر گره بیان‌گر هزینه F مرتبط به آن‌ است. در این مثال، ابتدا مقدار «آستانه» (Threshold) را ۳ در نظر می‌گیریم و گام‌های الگوریتم را طبق مراحل گفته‌شده طی می‌کنیم. در هر شاخه، عمق درخت را تا زمانی‌که هزینه F گره‌ها از مقدار آستانه بزرگتر نباشد، پیموده و هزینه F هر گره‌ای که از مقدار آستانه بزرگ‌تر باشد را نگه می‌داریم. این مرحله تا زمانی ادامه می‌یابد که تمامی گره‌های دارای هزینه $$F<Threshold$$، گسترش یابند. سپس پیمایش الگوریتم دوباره از گره ریشه، شروع می‌شود با این تفاوت که این بار کم‌ترین هزینهF – که در تکرار قبلی حفظ شده است – به‌عنوان مقدار آستانه انتخاب می‌شود. به این ترتیب، مراحل الگوریتم تا هنگام دستیابی به هدف یا گسترش تمامی گره‌ها ادامه می‌یابد.

مزایا و معایب الگوریتم *IDA

تا این قسمت از مطلب یاد گرفتیم که الگوریتم *IDA چیست. حال می‌خواهیم با مزایا و معایب این الگوریتم آشنا شویم.

مزایای الگوریتم *IDA

در فهرست زیر، مزایای این الگوریتم را آورده‌ایم.

• بهینه بودن: الگوریتم *IDA تنها در صورت به‌کارگیری تابع هیوریستیک دارای مقبولیت، کوتاه‌ترین مسیر را پیدا می‌کند.
• کامل بودن: در صورت وجود حداقل یک راه حل، این الگوریتم‎ حتماٌ آن را پیدا خواهد کرد.
• استفاده بهینه از حافظه: IDA*‎ در یک زمان، تنها یک مسیر را در حافظه ‌نگهداری می‌کند.
• انعطاف‌پذیری: بسته به کاربرد مورد نظر، این الگوریتم، تعدادی از توابع هیوریستیک را مورد استفاده قرار می‌دهد.
• کارایی: این روش گاهی اوقات از سایر روش‌ها نظیر جست و جوی اول سطح و جست و جوی هزینه یکنواخت، بهتر عمل می‌کند.

معایب الگوریتم *IDA

برخی از معایب این الگوریتم را نیز در ادامه بیان کرده‌ایم.

•  این الگوریتم، گره ملاقات شده را بارها و بارها گسترش می‌دهد. همچنین مسیر پیمایش شده برای گره‌هایی که ملاقات کرده است را ذخیره نمی‌کند.
• روش بیان شده، ممکن است از سایر روش‌ها همچون A*‎ یا جست و جوی اول سطح، در پیداکردن راه‌حل کندتر عمل کند، زیرا به دفعات عملیات ملاقات و گسترش یک گره را تکرار می‌کند.
•  این الگوریتم نسبت به روش A*‎ نیاز به زمان و قدرت پردازش بالاتری است.

پیاده‌ سازی الگوریتم *IDA

در این قسمت، شبه‌کد و پیاده‌سازی الگوریتم *IDA در پایتون را آورده‌ایم.

شبه کد الگوریتم *IDA

در ادامه شبه کد الگوریتم *IDA را بیان کرده‌ایم.

root=initial node;
Goal=final node;
function IDA*()                                             //Driver function
{

threshold=heuristic(Start);
while(1)             //run for infinity
{

integer temp=search(Start,0,threshold); //function search(node,g score,threshold)
if(temp==FOUND)                                 //if goal found
         return FOUND;                                             
if(temp== ∞)                               //Threshold larger than maximum possible f value
         return;                               //or set Time limit exceeded
threshold=temp;

}

}
function Search(node, g, threshold)              //recursive function
{

f=g+heuristic(node);
if(f>threshold)             //greater f encountered
         return f;
if(node==Goal)               //Goal node found
         return FOUND;
integer min=MAX_INT;     //min= Minimum integer
foreach(tempnode in nextnodes(node))
{

//recursive call with next node as current node for depth search
integer temp=search(tempnode,g+cost(node,tempnode),threshold);  
if(temp==FOUND)            //if goal found
return FOUND;
if(temp<min)     //find the minimum of all ‘f’ greater than threshold encountered                                min=temp;

}
return min;  //return the minimum ‘f’ encountered greater than threshold

}
function nextnodes(node)
{
             return list of all possible next nodes from node;
}

پیاده‌سازی الگوریتم *IDA در پایتون

در بخش قبل با شبه کد این الگوریتم آشنا شدید، حال دراین قسمت پیاده‌سازی الگورریتم IDA*‎ را با زبان برنامه نویسی پایتون معرفی کرده‌ایم که در توضیحات کد، مراحل پیاده‌سازی به خوبی بیان شده است.

def iterative_deepening_a_star(tree, heuristic, start, goal):
    """
    Performs the iterative deepening A Star (A*) algorithm to find the shortest path from a start to a target node.
    Can be modified to handle graphs by keeping track of already visited nodes.
    :param tree:      An adjacency-matrix-representation of the tree where (x,y) is the weight of the edge or 0 if there is no edge.
    :param heuristic: An estimation of distance from node x to y that is guaranteed to be lower than the actual distance. E.g. straight-line distance.
    :param start:      The node to start from.
    :param goal:      The node we're searching for.
    :return: number shortest distance to the goal node. Can be easily modified to return the path.
    """
    threshold = heuristic[start][goal]
    while True:
        print("Iteration with threshold: " + str(threshold))
        distance = iterative_deepening_a_star_rec(tree, heuristic, start, goal, 0, threshold)
        if distance == float("inf"):
            # Node not found and no more nodes to visit
            return -1
        elif distance < 0:
            # if we found the node, the function returns the negative distance
            print("Found the node we're looking for!")
            return -distance
        else:
            # if it hasn't found the node, it returns the (positive) next-bigger threshold
            threshold = distance


def iterative_deepening_a_star_rec(tree, heuristic, node, goal, distance, threshold):
    """
    Performs DFS up to a depth where a threshold is reached (as opposed to interative-deepening DFS which stops at a fixed depth).
    Can be modified to handle graphs by keeping track of already visited nodes.
    :param tree:      An adjacency-matrix-representation of the tree where (x,y) is the weight of the edge or 0 if there is no edge.
    :param heuristic: An estimation of distance from node x to y that is guaranteed to be lower than the actual distance. E.g. straight-line distance.
    :param node:      The node to continue from.
    :param goal:      The node we're searching for.
    :param distance:  Distance from start node to current node.
    :param threshold: Until which distance to search in this iteration.
    :return: number shortest distance to the goal node. Can be easily modified to return the path.
     """
    print("Visiting Node " + str(node))

    if node == goal:
        # We have found the goal node we we're searching for
        return -distance

    estimate = distance + heuristic[node][goal]
    if estimate > threshold:
        print("Breached threshold with heuristic: " + str(estimate))
        return estimate

    # ...then, for all neighboring nodes....
    min = float("inf")
    for i in range(len(tree[node])):
        if tree[node][i] != 0:
            t = iterative_deepening_a_star_rec(tree, heuristic, i, goal, distance + tree[node][i], threshold)
            if t < 0:
                # Node found
                return t
            elif t < min:
                min = t

    return min

سوالات متداول

در ادامه سوالات متدوال را پیرامون الگوریتم *IDA بیان کرده‌ایم.

مثال الگوریتم IDA‎*‎ در دنیای واقعی چیست؟

از نمونه‌های الگوریتم IDA‎*‎ می‌توان به مواردی همچون مسیریابی، زمان‌بندی و غیره اشاره کرد، برای مثال حل مکعب روبیک نمونه‌ای از یک مسئله برنامه‌ریزی است که با این الگوریتم قابل‌ حل است.

تفاوت الگوریتم *IDA و A*‎ چیست؟

الگوریتم *IDA نوعی جست‌ و جوی عمقی تکرار شونده است که همانند الگوریتم A*‎ از تابع هیوریستیک برای تخمین هزینه برای رسیدن به هدف استفاده می‌کند. این الگوریتم به دلیل استفاده از DFS، در مقایسه با A*‎ از حافظه کمتری استفاده می‌کند. همچنین به دلیل استفاده از جست و جوی DFS، حافظه مصرفی الگوریتم *IDA نسبت به A*‎ کمتر است. اما بر خلاف روش جست و جوی عمقی تکرار شونده به صورت آگاهانه عمل می‌‌کند و بنابراین در همه جای درخت جست و جو به عمق یکسان نمی‌رود.

جمع‌بندی

در این مطلب از مجله فرادرس، مرور کوتاهی بر الگوریتم‌های جست‌ و جو داشتیم و یاد گرفتیم که IDA*‎ چیست. همچنین بیان کردیم که الگوریتم *IDA، یکی از الگوریتم جست و جوی آگاهانه است که مزیت‌های الگوریتم جست و جوی ‌DFS و الگوریتم A*‎ را با هم ترکیب می‌کند.

هدف این الگوریتم یافتن راه‌حل بهینه و در عین حال به حداقل رساندن استفاده از حافظه است. با افزایش مرحله به مرحله مقدار آستانه برای جست و جوی عمقی، الگوریتم *IDA فضای جست و جو را به صورت مؤثر بررسی و تضمین می‌کند که در صورت وجود راه‌حل بهینه، آن را پیدا می‌کند. با این حال ممکن است از نظر پیچیدگی زمانی به اندازه سایر الگوریتم‌ها کارآمد نباشد. به‌طور کلی، الگوریتم *IDA ابزاری ارزشمند برای حل مسائل جست و جو است که در آن به‌کارگیری زیاد از حافظه، نگران‌کننده است و یافتن راه حال بهینه اهمیت زیادی دارد. در ادامه، مزایا و معایب الگوریتم *IDA را برشمردیم و در آخر نیز شبه کد و پیاده‌سازی الگوریتم *IDA را بیان کردیم.